CHEMISTRY
Look at the ELEMENTS. There ARE distinct kinds, 96 of them have been discovered to occur naturally and we've been able to smash together 16 more. It is not clear whether there is a limit to how many we can make.. Why isn't there just a random mush of protons and electrons in the world? Why does the universe break up into discrete chunks of matter to begin with? Once you get discrete protons and electrons with their properties, mathematics gives us the rest.
Or look at the MINERALS. There are over 4000 amazing different forms.
http://www.uwgb.edu/dutchs/EarthSC202Notes/minerals.htm
working with this database:
http://rruff.info/ima/
starting with the 12 most abundant elements on the earth's crust:
O , Si , Al , Fe , Ca , Na , Mg , K , Ti , H , P , Mn, we get 842 minerals in this database
Why don't the elements combine higgledy piggledy like different colors of clay, mixing, mixing until it's all grey? Because the atoms are discrete and the quantum mechanics, the discrete charges, the mathematics again gives us only certain discrete combinations. Only half a dozen to a dozen ways nitrogen combines with oxygen. Iron ions come in +2 or +3 electrical charges and have a specific size. Ditto aluminum ions. Silicate networks come in a surprising but finite number of variations and they have negative electrical charges. These all get matched up into many hundreds of different discrete structures. These structures can even be modified by the environment in which they grow.
Now of course CARBON and NITROGEN.... ah that's capable of MORE combinations. Organic chemistry. MANY more. MILLIONS. But for each number of carbons in a molecule, only a fixed (though large) amount. So for instance starting at the bottom: one carbon: CO2, CO, CO3--, CH4, CH3OH, CH2O, CHOOH, maybe a FEW others, thats it, with C, O, H. So the physics and the math still gives us a bewildering array of discrete types, but not total chaos.
DYNAMIC STRUCTURES FROM HEAT FLOW
One more example of discreteness with physics. This time not at equilibrium but with ENERGY FLOW. There is a common misconception that the second law of thermodynamics tells us that every system eventually leads to disorder, less structure. The actual fact is that in any closed system the TOTAL disorder increases, but a SUBSYSTEM of that larger system can actually INCREASE its order at the expense of the rest of the system. For instance, take the solar system. It starts out highly ordered, structured: all the energy in the sun, the outer-space is cold. As the sun shines and energy flows from the sun to the rest of the cold universe the whole system becomes less ordered, eventually everything will be the same temperature no structure left. But it's that energy flow that makes all the exciting things on Earth happen: weather! Thus while the total system becomes less ordered, the Earth can become more ordered, more structures appear.
If you heat a shallow layer of water in a pan, at a low temperature you get random motions in the water molecules as they carry the heat (molecular motion) from the high temperature bottom of the pan to the low temperature surface of the water. On a macro scale what you begin to see is that the layer of water directly above the pan expands (gets warmer) and thus less dense than the layer above it and rises. This rising layer breaks up into blobs randomly. Of course if blobs are rising, blobs of water at the top must sink because they are more dense (cooler). Already the fact that these homogenous layers break up into blobs is curious math. In fact, I'm not sure we fully understand it (look up studies of water droplets and splashes, very complex!). The breaking up of the top layer into blobs as they descend, i think is mediated in a complex way by the surface tension of the water at the top. (the stuff that makes water creep up the edges of a container of water a millimeter or so, called the meniscus.
As you raise the temperature of the bottom of the pan relative to the top of the water you get more random motion. at a certain temperature difference, though, these rising and falling blobs eventually arrange themselves (surprise!) into a fairly neat hexagonal array of convection cells. Warm water rises in the center of each cell and falls at the edges. This is called Benard convection.Pictures here:
http://www.intothecool.com/complex.php
(this website (and book) OUGHT to be an ideal introduction to this stuff. Alas it is POORLY written. (someone help me write a better one)
This also happens in the extremely thin layer of atmosphere on earth.
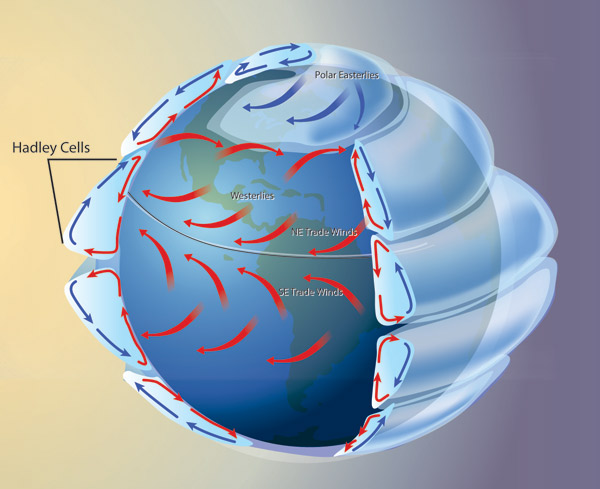
GLOBAL ATMOSPHERIC CIRCULATION PATTERNS.
HEAT FLOW ON SPINNING OBJECTS
The next spin we can introduce to the story IS spinning. If you put a rotating cylinder inside another rotating cylinder and fill the space between them with fluid a similar thing happens. As you increase the relative speeds various discrete numbers of fluid rolls form:
Video here:
https://www.youtube.com/watch?v=cEqvx0N_txI
Now combine these two continuous operations: spinning boundaries and convection. Have a spherical planet rotating underneath a thin atmosphere. Have the sun heat the surface of the planet relative to the cooler top of the atmosphere, and you get our pattern of atmospheric circulation:
http://upload.wikimedia.org/wikipedia/commons/thumb/6/6d/Earth_Global_Circulation.jpg/300px-Earth_Global_Circulation.jpg
But the Earth is not just a rotating cylinder, it's a rotating sphere, and since the equator is longer around then circles of latitude north and south, it is also zipping by under the atmosphere at a faster velocity than the ground is north and south. This difference in velocity causes the Hadley cells in the atmospheric circulation to break up into discrete masses of air rotating across the land in clockwise and anticlockwise directions:
http://en.wikipedia.org/wiki/File:Coriolis_effect14.png
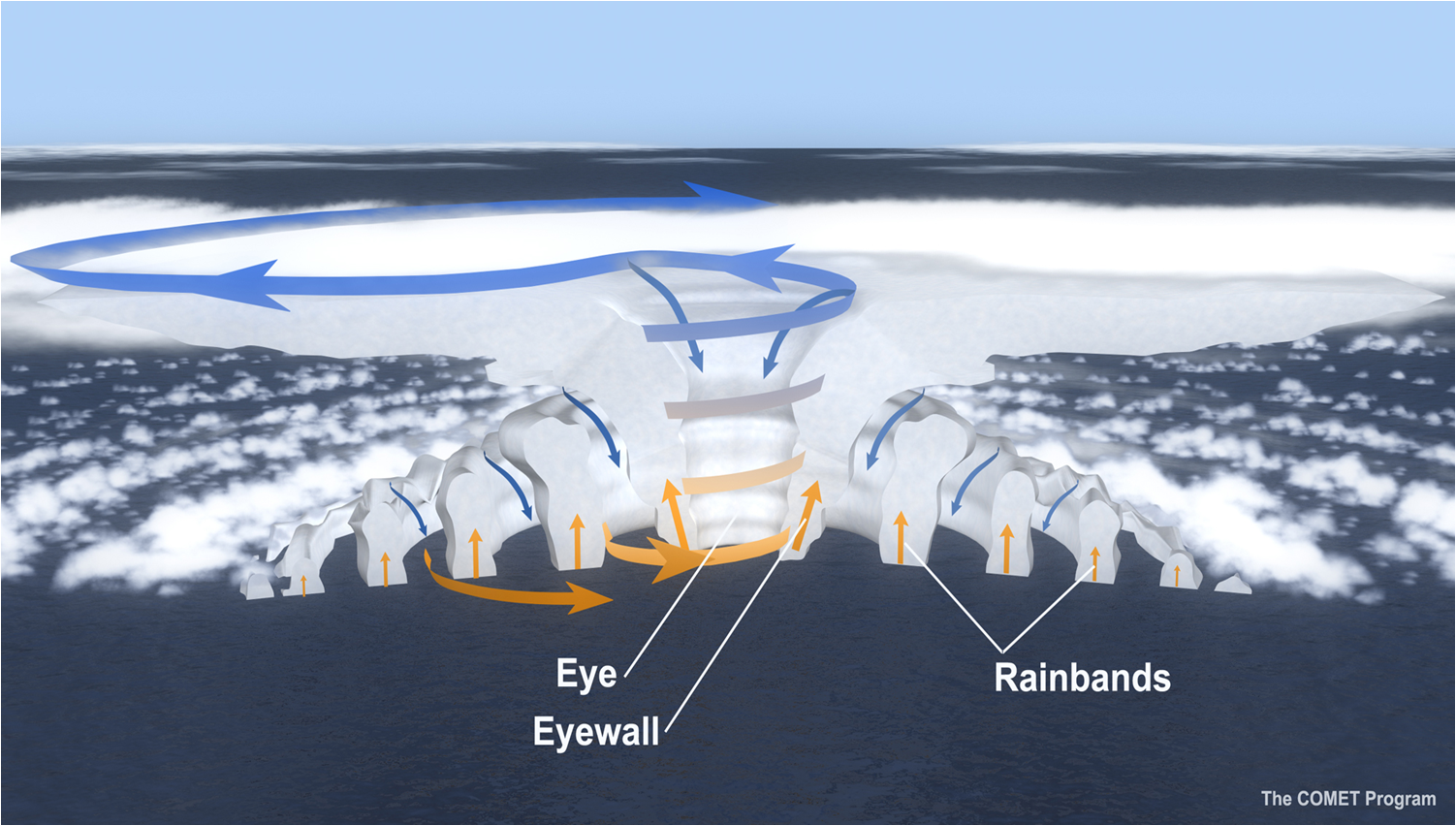
Now add the complication of the fact that when you cool moist air it breaks up into DISCRETE tiny droplets of water (surface tension again! And a whole other example: why when we lower the temperature of water continuously does it all of a sudden at 32 degrees make a radical change in form?) or ice, which then fall... and you get weather! Discrete high and low pressure cells gyrating in opposite directions. In extreme cases you can get distinct creatures which can last for many days called hurricanes
JUPITER
The great red spot of Jupiter is one of many storm cells. Some last for years, the red spot has so far lasted a couple hundred years at least. (actually i'm conbobulating three kinds of structures here: the taylor vortices, the Benard cells, the complex thing a terrestrial storm cell is, and turbulence vortices. (hah! are there distinct types here? do they all blend? ) ) not 100% sure which the red spot is, or maybe a combination.. Already there is much complication before we even get to biological evolution!
Pictures of discrete weather patterns on Jupiter.
DYNAMIC STRUCTURES FROM CHEMISTRY
FIRST, COMBINING SURFACE TENSION AND CHEMISTRY TO GET THE MERCURY BEATING HEART:
We all know that Iron rusts, and wood burns. These are spontaneous reactions that give off energy. They happen because plants separate out carbon and the oxygen from carbon dioxide. With the carbon they make wood, the oxygen they put into the atmosphere. This is a state of high potential energy just as in when the sun evaporates water from the ocean , it is ready to fall from the sky as rain and do work, the wood and oxygen are ready to burn and do work.
We do a similar thing when we separate out Iron oxide ore into iron metal and oxygen.
Just as in our previous examples of pattern formation from energy flow, rusting can also produce pattern in certain systems. Here we have a simple system of just 5 different chemicals: Iron nail, mercury blob, sulfuric acid in water and potassium dichromate.
Just as iron will spontaneously rust when moist, this iron nail will rust in the acid solution of dichromate (only faster). This reaction releases energy. What we do is put the mercury blob in between and the surface tension of the blob causes all the fun.
Mercury has a high surface tension like water drops on a waxy surface. Now the dichromate will rust the mercury blob. The layer of rust has low surface tension and the blob spreads out, and touches the nail. The mercury rust in some ways isn't 'as rusted' as iron rust (there is still more chemical potential energy in it relative to iron rust) and so the mercury rust will rust the iron nail, in the process it unrusts and turns back to pure mercury. When it does so, it has more surface tension and so pulls back into a blob and lets go of the nail. Now no longer touching the iron nail, it can get rusted by the dichromate again and the process repeats. The system oscillates.
Just as the overall flow of heat in our Benard cells and weather systems interact with fluids to produce patterns of convection cells, here the overall flow of energy from unoxidized materials to oxidized materials interacts with the surface tension to produce patterns of oscillation.
mercury blob oscillator.
NEXT WE COMBINE DIFFUSION AND CHEMISTRY IN THE BELOUSOV ZHABOTINSKY REACTION
Let's take 4 chemicals dissolved in water, mix them into a petri dish and see what happens:
0.2 Molar solution of Malonic Acid, 0.3 Molar solution of Sodium Bromate, 0.3 Molar solution of Sulfuric Acid, and .005Molar solution of Ferroin
here's how it's done:
Combine to form a solution. Add approximately 5 mL of the solution to a Petri dish, 6 cm in diameter, so that the thickness of the layer is 0.5 -1 mm. Watch until colorful spatio-temporal patterns emerge.
the malonic acid is a simple sugar from plants, like beets. sodium bromate and sulfuric acid are rather simple compounds to make. The ferroin is Iron combined with a rather clever organic molecule. the Iron takes part in the reaction, the organic molecule: phenanthroline is a cheat, we put it there only to make the pretty colors so we can see what the iron is doing, it changes from red to blue depending on the state of the iron in the reaction. The reaction would go without the phenanthroline, the colors just wouldn't be as easy to see.
Here is what happens:
This is similar to our previous example. The Malonic acid is an organic molecule, like wood. It can be oxidized by the bromate all the way back to Carbon dioxide, similar to the way wood burns. This oxidation or rusting, again gives off energy and that energy flow is what drives the reaction. For instance we can simply drip concentrated sulfuric acid on a pile of sugar and it will vigorously burn it back to Carbon dioxide and carbon char. The bromate does this a little slower, and causes no burning.
Again like our mercury beating heart we will put another substance in between the bromate and the malonic acid. The iron in the ferroin will play the role of the mercury blob in the previous example. This reaction is much more complicated and I don't completely understand it. Dozens of intermediate chemicals and reactions take place. The upshot is this:
The bromate oxidizes the iron first, that changes it's color. Then the oxidized iron will oxidize the malate, and in return get unoxidized back to it's other color state. Here is where the diffusion plays a role. these two different reactions take place at different rates and this interacts with the different states of the chemicals diffusing across the wave fronts at different rates and this is what ultimately causes the waves of color change to occur.
I think this process has been fairly well understood, but I have not mastered it yet. The math is complicated!
more info about this Belousov-Zhabotinsky (or BZ) reaction here
WE CAN EVEN COMBINE CONVECTION AND CHEMISTRY AND GET A FLAME
Here are some of the chemical reactions that begin to occur even when we burn the simplest fuel: methane CH4:
So we see, way before biology, evolution and human creativity happen, physics already gives us so many ways to create discrete complex entities.
EVEN MATH ALONE GIVES COMPLEXITY
But who needs physics? Even MATH will even give us discrete types for free:
Given the simple laws of 3 dimensional geometry, how many REGULAR POLYHEDRA can we make, where each face is an identical regular polygon and each vertex where they meet is identical? I.e. a pyramid out of four equilateral triangles, or a cube out of 6 squares? The surprise is that we can only make FIVE such discrete figures: pyramid (tetrahedron), double pyramid (octohedron, 8 triangles) , cube, dodecahedron (12 pentagons) , and icosahedron (20 triangles). We get a curious dollop of discrete complexity but not an infinite amount of chaos.
http://www.cut-the-knot.org/do_you_know/polyhedra.shtml
(with simple proof of this fact!)
http://mathforum.org/sum95/math_and/poly/reg_polyhedra.html
This happens often in math. you propose a simple set of rules and follow them through and you end up with a sometimes bewildering variety of discrete, but not infinitely chaotic set of structures.
PRIME NUMBERS
Another example is the PRIME NUMBERS. They are simple to define: a whole number that has only itself and 1 as factors, i.e. 7=7X1 and 13=13X1 are prime but 12=2X6=3X4 is not.
So with that simple definition what do we get? The further out you go into bigger numbers the more factors there are to divide into them so the primes start dwindling: there are more primes between 2 and a 100 then between 1000 and 1100. Do they dwindle out all together? No. A simple proof shows us that there are a infinite number of them.
(I should give the proof huh?)
Is there any pattern to them? 2 3 _ 5 _ 7 _ _ _ 11 _ 13 _ _ _ 17 _ 19 _ _ _23 _ _ _ _ _ 29 _31 _ _ _ _ _ 37 _ _ _41 _ 43... The gaps are funny. Is it chaotic or is there a pattern?
One pattern is that some primes come in pairs! 11, 13; 17, 19; 41, 43. does THAT keep happening? Actually it's been 2500 years and no one has figured out a proof of it. With computers we've calculated that it keeps happening WAY WAY out there...
Another odd set of discrete creatures is the CLASSIFICATION OF FINITE SIMPLE GROUPS:
My description:
http://blackskimmer.blogspot.com/2007/03/classification-of-finite-simple-groups.html
This:
http://plus.maths.org/issue41/features/elwes/index.html
isn't bad, but STILL doesn't give enough examples to give a gut feel.
Here only ONE group is described:
http://plus.maths.org/issue39/features/colva/index.html
Advanced summary:
www.ams.org/notices/199502/solomon.pdf
And here, Conway himself itching to know what on earth is going on:
https://www.youtube.com/watch?v=jsSeoGpiWsw
DYNAMICAL SYSTEMS
Now, those were static structures, what happens when we create DYNAMICAL mathematical systems?
JOHN HORTON CONWAY'S GAME OF LIFE
One of the first and most famous that was discovered is John Horton Conway's game of life. It was first explored on pencil and paper and is easy to describe. It is a great mystery that the ancient Greeks, or Arabic mathematicians did not discover it, nor did the classical European mathematicians and scientists. It is is very new. 1970s! Try to figure out yourself before looking at pretty pictures:
http://blackskimmer.blogspot.com/2007/07/john-horton-conways-game-of-life-here.html
LANGTON'S ANT
another even simpler example is Langton's ant: on a 100x100 grid of white squares you place a very simple mechanism onto one square. it keeps repeating a very simple motion: if the square is white turn 90 degrees clockwise, if black, 90 degrees counterclockwise, then flip the color of the square and move one square foward. repeat. what do you think might happen?
more elaborate video:
http://www.youtube.com/watch?v=1X-gtr4pEBU
How does such a simple rule generate such a complex pattern for so long before it settles down into another pattern? This simple rule counts up to 9,978 steps before it settles down into a shifting repeating pattern of 104 steps each that creates the final repetitive highway.
Note that this is such a simple mechanism that surely we can find a simple molecule that does this on the regularly spaced atoms of a crystal surface!
This is a stark example of a very simple mechanism that creates a long range complex order. Traditional human history has it that complex creativity can only come from a more complex mind, not mere simple molecular rules! Where in this simple rule was the number 9,978 embedded?
One can explore DOZENS of varieties of rules like this and see what kind of structures they crate. Maybe we can let loose a couple a thousand or million of these molecules together and see what massive complexity they can create?
MORE
my ongoing attempt at organizing all these examples:
http://complexitylabs.blogspot.com/2009/04/complexity-lab-manual.html
No comments:
Post a Comment